Apolonio I.20

Como, en una parábola, por definición, los cuadrados sobre las ordenadas son iguales a los rectángulos formados por el lado recto constante y el segmento en el diámetro entre el vértice y el extremo de la ordenada, los cuadrados sobre las ordenadas serán entre sí como los segmentos en el diámetro, por Euclides VI.1.
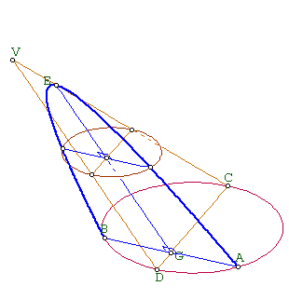
Podemos expresar el resultado, para la figura adjunta, como .
Este resultado es la proposición I.20 de las Cónicas.
En lugar de la expresión anterior escribiremos , pero se debe recordar que ninguno de los términos es un número, sino una superficie o un segmento y no se trata ni de fracciones ni de una igualdad entre números, sino de una proporción.
Subir




Deja una respuesta