El área de la cicloide

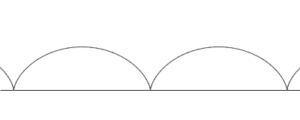
Si un polígono regular de $n$ lados rueda sobre una recta base, un vértice situado en la base termina por volver a la base después de describir una serie de $n-1$ arcos.
Uniendo con segmentos los extremos de cada uno de esos arcos se forma una línea poligonal (roja en la figura), de $n-1$ segmentos, que empieza y termina en la base y a la que llamaremos cicloide poligonal generada por el polígono regular.

Sea cual sea el número de lados del polígono regular que rueda, el área entre la cicloide poligonal y la base es el triple del área del polígono regular. (Maupertuis, 1727)

En consecuencia el área de la cicloide es el triple del área del círculo que la genera, que se puede considerar como un polígono de infinitos lados.

Demostración:
Descomponemos el área bajo la cicloide poligonal en dos partes.
Una formada por el área de los triángulos (azules) que tienen por vértices los extremos y el centro de cada arco recorrido por el vértice al rodar el polígono, es decir sus lados son un segmento de la cicloide poligonal y dos diagonales iguales del polígono, y la otra formada por el área de los triángulos (naranjas) restantes.

Estos triángulos (naranjas) restantes tienen por lados un lado del polígono y dos diagonales consecutivas, de las trazadas desde un vértice, y es claro que su área total es igual a la del polígono que genera la cicloide poligonal.

Basta entonces con demostrar que el área total de los triángulos (azules) que tienen un lado en la cicloide poligonal es el doble de la del polígono rodante.

Esos triángulos son isósceles, semejantes entre sí y semejantes al triángulo formado por un lado del polígono y dos radios de la circunferencia circunscrita.
Los lados iguales de esos triángulos isósceles son iguales a las sucesivas diagonales trazadas desde un vértice del polígono regular.

Designamos con $d_1,\ldots, d_{n-1}$ las sucesivas diagonales trazadas desde un vértice ( $d_1$ y $d_{n-1}$ son los lados adyacentes al vértice) de un polígono de $n$ lados, con $T_k$ el área del triángulo que tiene dos lados iguales a $d_k$ y el otro en la cicloide, con $T$ el área del triángulo cuyos vértices son el centro del polígono y los extremos de un lado, y con $R$ el radio de la circunferencia circunscrita.

Como las áreas de figuras semejantes son entre sí como los cuadrados de segmentos correspondientes (Euclides VI.20), $\dfrac {T_k}{T} = \dfrac{d_k^2}{R^2}$ , y la suma de las áreas de los triángulos (azules) $T_k$ será $\sum T_k = \dfrac{T}{R^2} \sum d_k^2$ .
Pero en la entrada anterior demostramos que $\sum d_k^2 = 2nR^2$ , y por tanto $\sum T_k = 2nT$ , que es el doble del área del polígono regular.

Por tanto el área entre la cicloide poligonal y la base es el triple del área del polígono regular que la genera.

Entradas relacionadas:

Deja una respuesta Cancelar la respuesta